Spherical Coordinates
A coordinate system based on a sphere, typically using latitude and longitude to specify locations on the Earth.
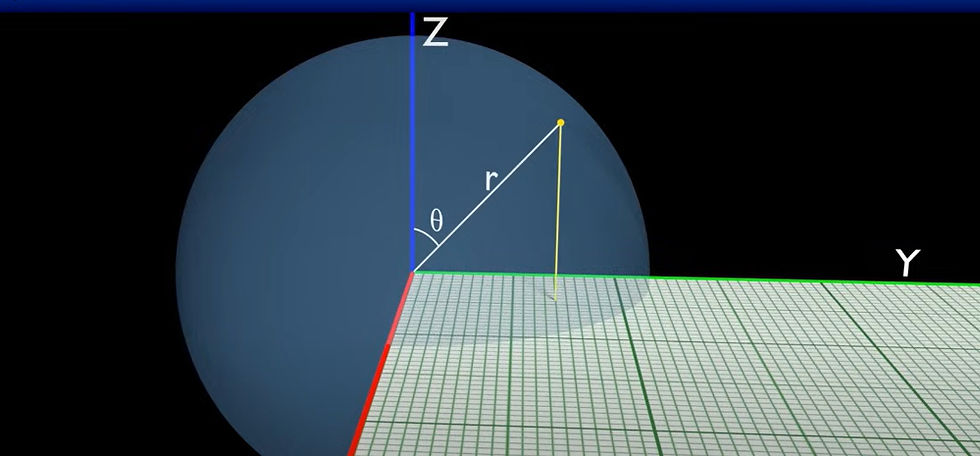
Define Spherical Coordinates
Three values—a radius and two angles—are used to represent points in three-dimensional space using spherical coordinates. Particularly helpful for places on or close to a sphere, such as Earth, is this system.
The definition of a point in the spherical coordinate system is as follows:
Radius (r) is the distance between the point and the origin, or the sphere's centre.
The polar angle, also known as the zenith angle, is the angle formed by the point and the positive vertical axis (θ).
Measured from a reference direction (often the x-axis), the azimuthal angle (φ) is the angle of rotation around the vertical axis.
Related Keywords
The spherical coordinate system represents a point in 3D space using its distance from the origin (r), the angle from the z-axis (\theta), and the angle in the xy-plane (\phi).
Spherical coordinates use radius, polar angle, and azimuthal angle to extend polar coordinates, which define a point by its distance from the origin and an angle, to three dimensions.
Cartesian to spherical conversion changes (x, y, z) into (r, \theta, \phi), where r = \sqrt{x^2 + y^2 + z^2}, \theta = \arccos(z/r), and \phi = \arctan2(y, x). It’s useful for problems with radial symmetry.
In astronomy, GPS, navigation, and map-making, spherical geometry is used to study figures on a sphere, model planets, and determine the shortest routes.
